NCEES Civil PE Specification III.D.: Bearing Capacity
Problem
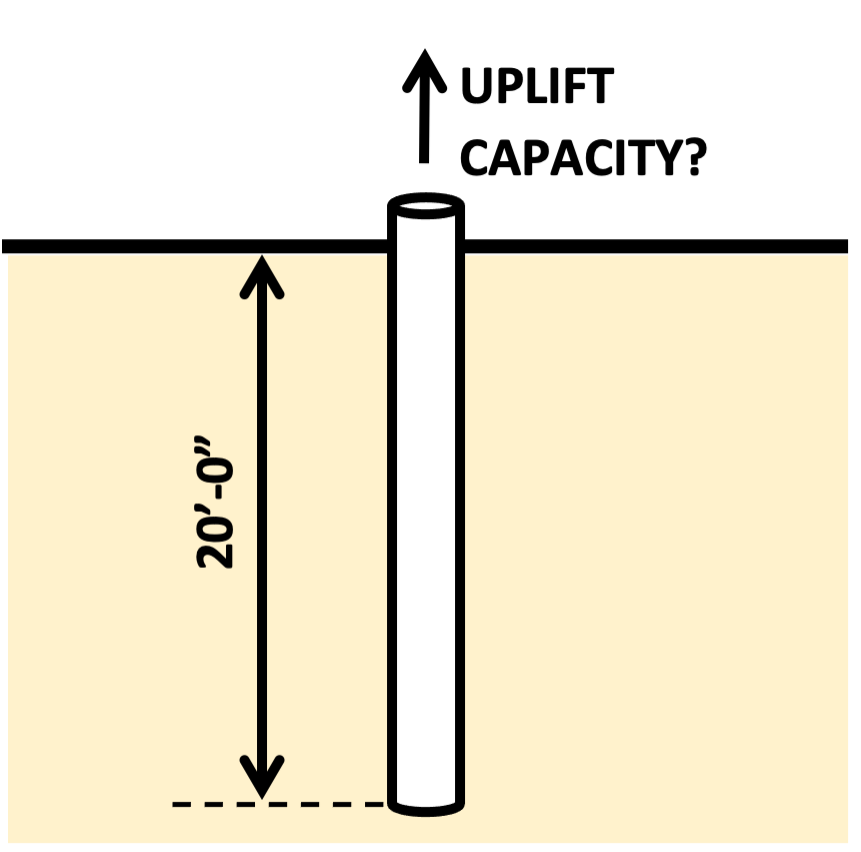
A 3-foot diameter Cast-In-Drilled-Hole pile is installed in a saturated clay layer to a depth of 20 feet. The soil was found to have an undrained shear strength of 2 ksf at the surface and 4 ksf at a depth of 20 feet, varying linearly. Given a shaft weight of 20 kips and an adhesion factor α of 0.55, determine the uplift capacity of the shaft.
Select an Answer:
CORRECT 😃
INCORRECT 😟
% Students Correctly Answered:
40.4%
Solution
Answer: B) 331 kip
Uplift capacity is based on the skin friction and weight of a pile:
$$ Q_u=Q_s+W $$
Determine the skin friction capacity:
$$ Q_s=A_s\ast\ f_s $$
Area of pile in contact with soil:
$$ A_s=\pi\ast\ d\ast\ L=\pi\ast3ft\ast20\ ft=188.5\ ft^2 $$
Skin friction factor:
$$ f_s=\alpha\ast\ c $$
Shear strength to cohesion c relationship:
$$ S=c+\sigma\tan{\phi} $$
Assume angle of internal friction equals zero for saturated clay undrained shear strength:
$$ \phi=0 $$
Accordingly, cohesion c is equal to undrained shear strength. Consider undrained shear strength based on average strength in soil layer:
$$ S=\frac{2\ ksf+4\ ksf}{2}=3\ ksf $$
$$ S=c $$
$$ c=3\ ksf $$
Calculate skin friction factor:
$$ f_s=0.55\ast3\ ksf=1.65 $$
Calculate skin friction capacity:
$$ Q_s=188.5\ ft^2\ast1.65=311\ kip $$
Calculate ultimate uplift capacity:
$$ Q_u=Q_s+W=311\ kip+20\ kip=331\ kip $$
