Practice Question: Time to Fill a Tank Based on Pipe Discharge
NCEES Civil PE Specification Hydraulics and Hydrology: Energy and/or continuity equation
Problem
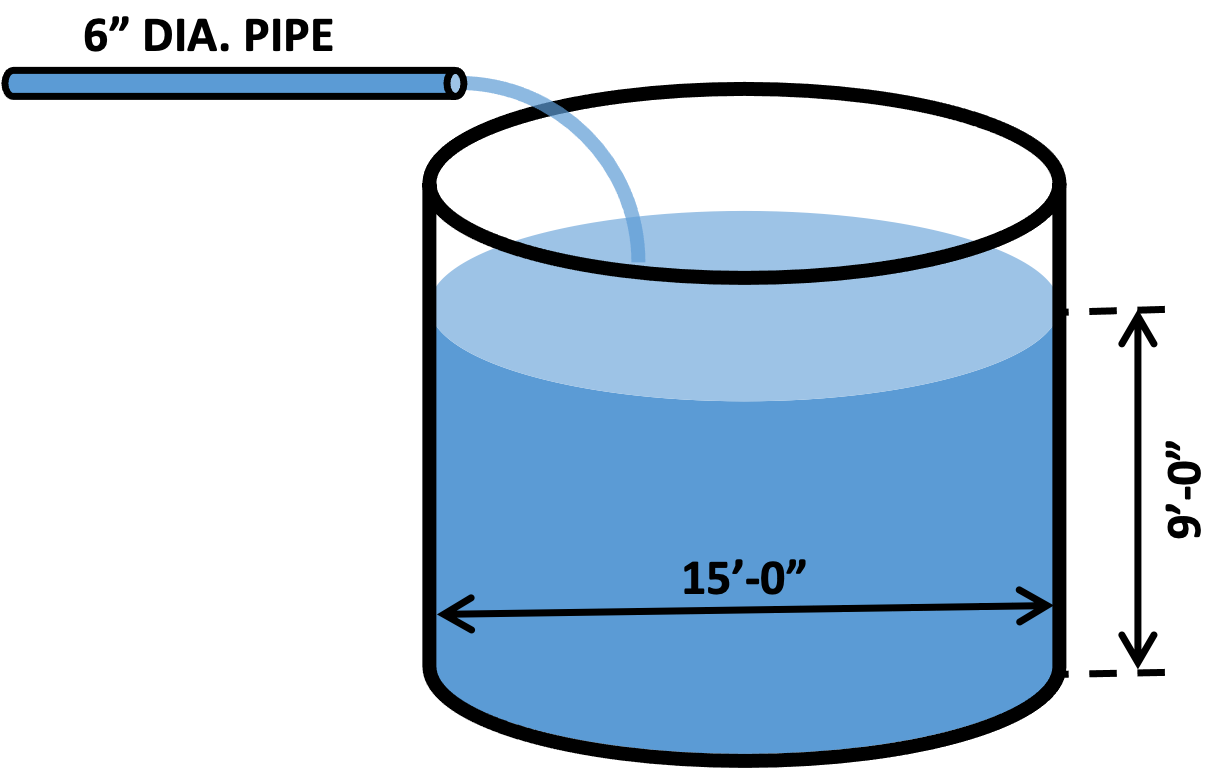
A 15-foot diameter open air tank is being filled by a 6-inch diameter water line to a depth of 9 feet. If the velocity of water exiting the pipe is 14 feet per second, approximately how long does it take to fill the tank?
Select an Answer:
CORRECT 😃
INCORRECT 😟
% Students Correctly Answered:
65.6%
Solution
Answer: A) 10 min
Calculate the rate of discharge of the 6 inch diameter pipe:
$$ Q=A\ast\ v $$
$$ A=\frac{\pi\ast d_{pipe}^2}{4} $$
where:
$$ Q=discharge\ rate\ in\ cubic\ feet\ per\ second $$
$$ v=discharge\ velocity\ in\ feet\ per\ second $$
$$ d_{pipe}=diameter\ of\ pipe $$
Solving for Q :
$$ A=\frac{\pi\ast\left(0.5\ ft\right)^2}{4}=0.2\ ft^2 $$
$$ Q=0.2\ ft^2\ast14\frac{ft}{s}=2.8\ \frac{ft^3}{s} $$
Time can be found by dividing volume to be filled by the rate of discharge:
$$ t=\frac{V}{Q} $$
where:
$$ V=volume\ in\ cubic\ feet $$
$$ Q=discharge\ rate\ in\ cubic\ feet\ per\ second $$
$$ t=time\ in\ minutes $$
Solving for V :
$$ V=\frac{\pi\ast d_{tank}^2}{4}\ast\ h $$
$$ V=\frac{\pi\ast\left(15\ ft\right)^2}{4}\ast\left(9\ ft\right)=1590.4\ ft^3 $$
Solving for t :
$$ t=\frac{V}{Q}=\frac{1590.4\ ft^3}{2.8\ \frac{ft^3}{s}}\ast\frac{1\ min}{60\ s}=9.5\ min $$
$$ t\ \approx10\ min $$
