Practice Question: Stationing along a Horizontal Curve
NCEES Civil PE Specification VI..: Basic circular curve elements
Problem
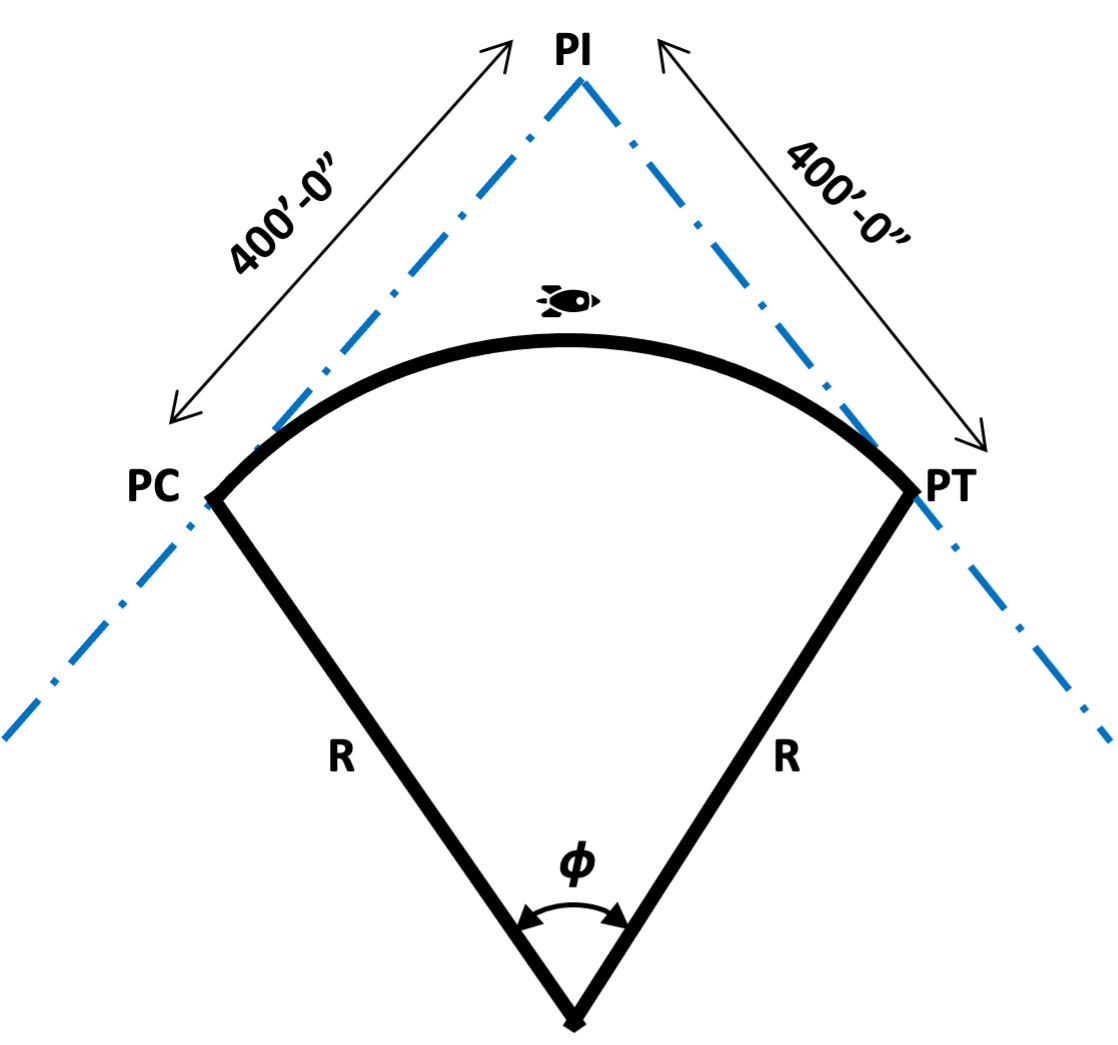
The year is 2045 and you are traveling along a newly constructed road in your electric hover craft. You enter a horizontal curve with a radius R of 900 feet and a tangent length T of 400 feet. Given the following figure and point of tangent PT at STA 25+00, determine the point of intersection for this curve.
Select an Answer:
CORRECT 😃
INCORRECT 😟
% Students Correctly Answered:
55.2%
Solution
Answer: B) STA 21+47
The location of the point of tangent (PT) can be related to the point of intersection, curve length, and tangent length through the following equation:
$$ STA\ PT\ =\ STA\ PI\ -\ T\ +\ L $$
where:
$$ STA\ PT\ =\ STA\ 25+00 $$
$$ T\ =\ 400\ ft $$
$$ L=\frac{2*π*R*ϕ}{360°} $$
Solve for length L by finding the intersection angle ϕ:
$$ ϕ=2\ast\tan^{-1}{\left(\frac{T}{R}\right)=2\ast}\tan^{-1}{\left(\frac{400\ ft}{900\ ft}\right)}=47.9° $$
$$ L=\frac{2*π*900 ft*47.9°}{360°}=752.8 ft $$
Solve for STA PI:
$$ STA\ 25+00=STA\ PI-400ft+752.8\ ft $$
$$ STA\ PI=STA\ 21+47 $$
